

In this case, our only alternative (aside from solving the complicated gas dynamics equations for the gas, which include the viscous stresses) is the explicitly specify the external force per unit area imposed by the surroundings. But, for an irreversible process, even though, by Newton's 3rd law, the force per unit area exerted by the gas on its surroundings is equal to the force per unit area exerted by the surroundings on the gas, the force per unit area exerted by the gas on its surroundings includes viscous stresses thus, the force can cannot be determined by simply applying the ideal gas law.

So, you are correct in saying that, for a reversible process, the internal pressure is equal to the external pressure. In this case the ideal gas law is recovered. Of course, at thermodynamic equilibrium, the rate of deformation of the gas is zero, and the force per unit area reduces to the pressure. The latter depend, not on the amount that the gas has been deformed, but on its rate of deformation. W PdVwhere limits of integration goes from V1to V2Putting for PK/V, and integrating we get,W (P1V1-P2V2)/(-1)(16) In and adiabatic process if W>0 i.e. The force per unit area exerted by the gas on the piston is comprised of two parts in an irreversible process: the local pressure and viscous stresses. In an irreversible process, the gas is not at thermodynamic equilibrium, so the ideal gas law will not apply. #=> color(blue)(q_(rev)) = -w_(rev) = color(blue)(+"1718.The ideal gas law (or any other equation of state) can only be applied to a gas at thermodynamic equilibrium. #cancel(DeltaU)^(0" for isothermal process") = q_(rev) + w_(rev)# So, the work involved the ideal gas exerting #"1718.3 J"# of energy to expand, due to the #"1718.3 J"# of heat it absorbed into itself: (however, one could use the ideal gas law to write #ln(V_2/V_1) = ln(P_1/P_2)# in this constant-temperature situation.) The work thus does not require the use the pressure of #"1 bar"#: At a particular constant temperature, the change of a substance, object or system is known as the Isothermal Process. The transfer of heat into or out of the system happens so slowly that thermal equilibrium is maintained. We keep in mind that the pressure did change, but we don't have an idea of how, off-hand. Find Work Done in Isothermal Process Calculator at CalcTown. An isothermal process is a thermodynamic process in which the temperature of a system remains constant. To Find: Work done Solution: Work done in isothermal reversible process is given by.
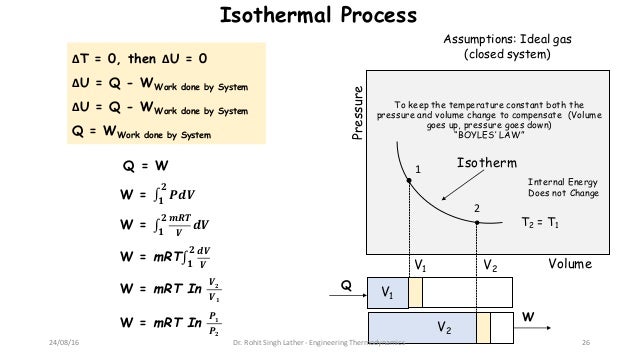
With the ideal gas law, we have that #PV = nRT#, or #P = (nRT)/V#. 3 moles of an ideal gas are expanded isothermally and reversibly from volume of 10 m 3 to the volume 20 m 3 at 300 K.

Thus, #w_(rev) -= -int PdV = -q_(rev)#, where work is done is from the perspective of the system and #q# is heat flow.Īll the reversible isothermal PV work #w_(rev)# done by an ideal gas to expand was possible by reversibly absorbing heat #q_(rev)# into the ideal gas.Ĭalculate the work performed in a reversible isothermal expansion by #1#mol# of an ideal gas from #22.7#L# to #45.4#L# at #298.15#K# and a #1#ba r# initial pressure. Hence, a reversible isothermal expansion is an infinitely-slow increase in volume at constant temperature.įor an ideal gas, whose internal energy #U# is only a function of temperature, we thus have for the first law of thermodynamics:


 0 kommentar(er)
0 kommentar(er)
